Polynomial Multiplication

작은 수의 곱은 컴퓨터에서 쉽게 처리할 수 있다.
하지만 큰 수의 곱은 컴퓨터에서 쉽게 처리하기 어렵기 때문에 큰 수는 Polynomial하게 처리하여
속도를 높일 수 있다.
여기서는 일반적인 Polynomial Multiply의 Time complexity를
Divide Conquer를 통해 줄이는 방법을 소개한다.

두 개의 다항식을 곱하는 상황을 고려해보면, 아래 그림과 같다.

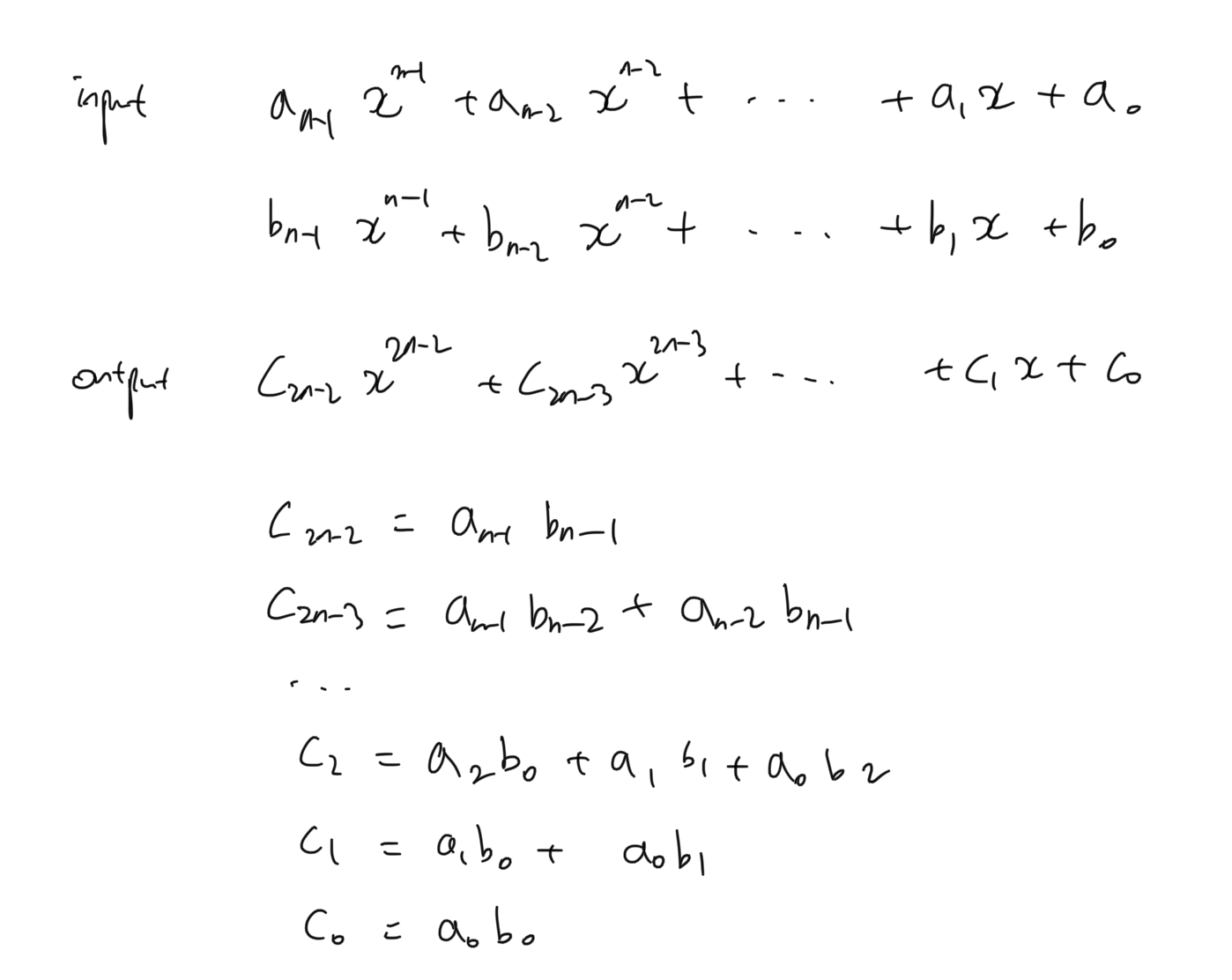
Naive

Naive한 방법으로는 이중 반복문을 통해 모든 수를 곱하고 더하는 방법이 있다.
하지만 이 방법은 이중 반복문을 사용하기 때문에 다항식의 개수 = n 일 때,
O(n^2) 이다.

Divide and Conquer

그림처럼 다항식을 반으로 나눈다. 그 후에 따로 계산된 값을 더하여 원하는 값을 출력한다.
(A(x) = D1, D0 / B(x) = E1, E0로 나누었다.)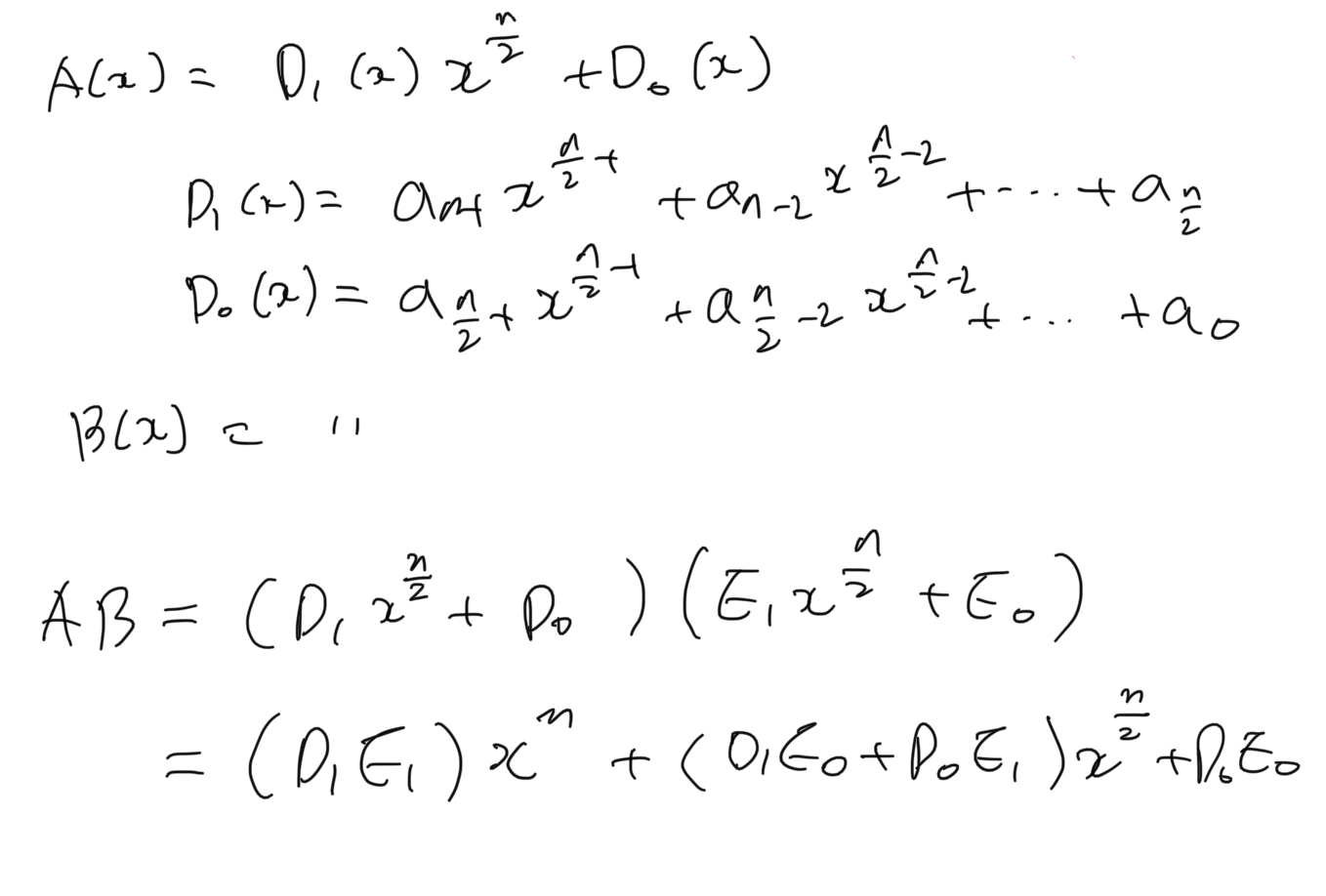

이 경우에는 보는 것 처럼 AB를 출력하기 위해 4가지의 하위 Task(D1E1, D1E0, D0E1, D0E0)
가 이루어 지고, 이를 합치기 위해 kn의 Task가 이루어진다.
즉, T(n) = 4 * T(n/2) + kn
이를 Master Theorem으로 계산해보면 O(n^2)이 나온다.
이는 Naive한 접근과 다르지 않다. 그렇다면 Divide Conquer가 소용이 없는것일까?

Karatsuba Divide and Conquer

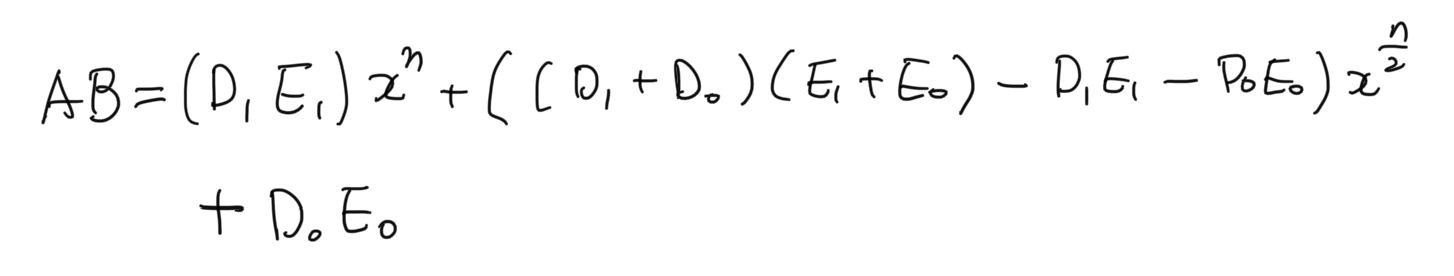
이 공식을 사용하면 4가지 Task가 아닌 3가지 Multiplication Task만 시행하면 된다.

• D1E1
• D0E0
• ( D1 + D0 )(E1 + E0)

T(n) = 3 * T(n/2) + kn 이므로,
O(n^(log_2(3)) = O(n^(1.58))이다.

Big Number Multiplication

312 * 514를 한다고 가정하면,
3 * 10^2 + 1 * 10 + 2 * 10^0
5 * 10^2 + 1 * 10 + 4 * 10^0

이를 다항식으로 계산하여 처리할 수 있다.