Master Theorem

Master Theorem은 Divide & Conquer(분할정복)에 사용되는 Theorem(정리)이다.
분할 정복에서는 재귀 호출 방식을 사용하는데 이 때 이 모든 연산 절차의 Time Complexity를
계산하는 일종의 공식이다.

T(n) = a * T( ceil( n / b )) + O(n^d)
이라고 가정했을 때, 세 가지 상황으로 구분되어 T(n)을 구할 수 있다.

• T(n) = O(n^d) if d > log_b(a)
• T(n) = O(n^d * log(n)) if d == log_b(a)
• T(n) = O(n^(log_b(a))) if d < log_b(a)

ex) T(n) = 4 * T(n/2) + O(n)
=> a = 4, b = 2, d = 1
=> log_b(a) = log_2(4) = 2
=> d < log_b(a)
=> T(n) = O(n^(log_b(a))) = O(n^2)

Proof

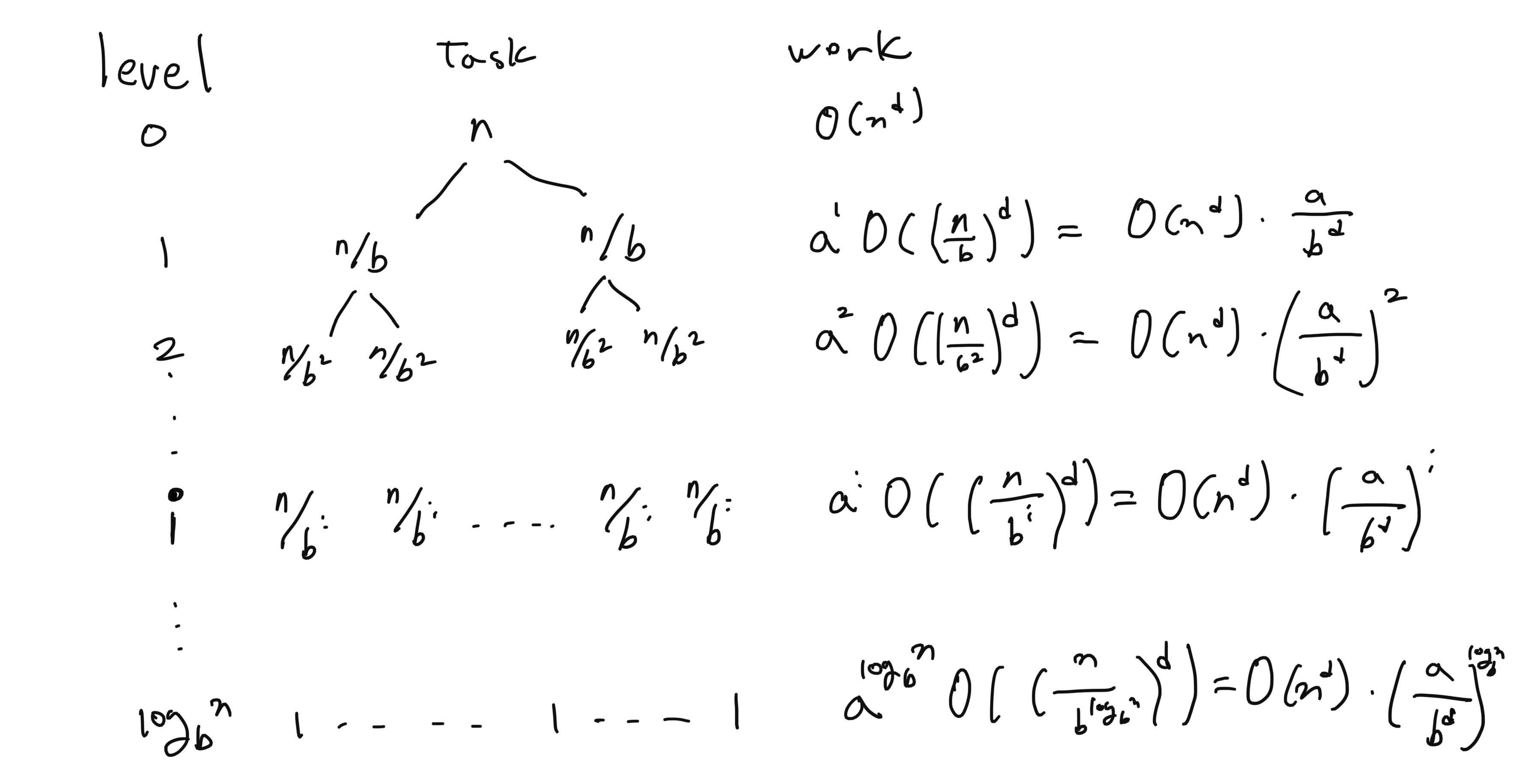
총 재귀되는 level은 ceil( log_b(n) )이다.
만약 n = 8일 때, 이분할하여(b=2) 연산 한다고 하면,
총 재귀의 level은 8 - (4, 4) - (2, 2, 2, 2) - (1, 1, 1, 1, 1, 1, 1, 1)
leve은 보는것처럼 시작이 level = 0 이라고 할 때,
총 level == 3으로 log_b(a) = log_2(8) = 3이다.
즉 재귀 level 은 log_b(n) 이다.
각 재귀로 호출 되는 Task 들의 관계(T(n) = a * T(n/b) + O(n^d))를 계산하면,
이 모든 work의 합은 등비수열 합의 공식으로 구할 수 있다.
등비수열의 합 공식은 곱해지는 수에 따라 결과값이 바뀌므로 아래와 같은 세 가지 상황으로 구분되게 된다.

• r == 1
• r > 1
• r < 1

r = (a/b^d) 이므로, Master Theorem 공식처럼

• d > log_b(a)
• d == log_b(a)
• d < log_b(a)

세 가지로 구분된다.

d > log_b(a)

등비수열 합 공식에 따라서 아래와 같다.

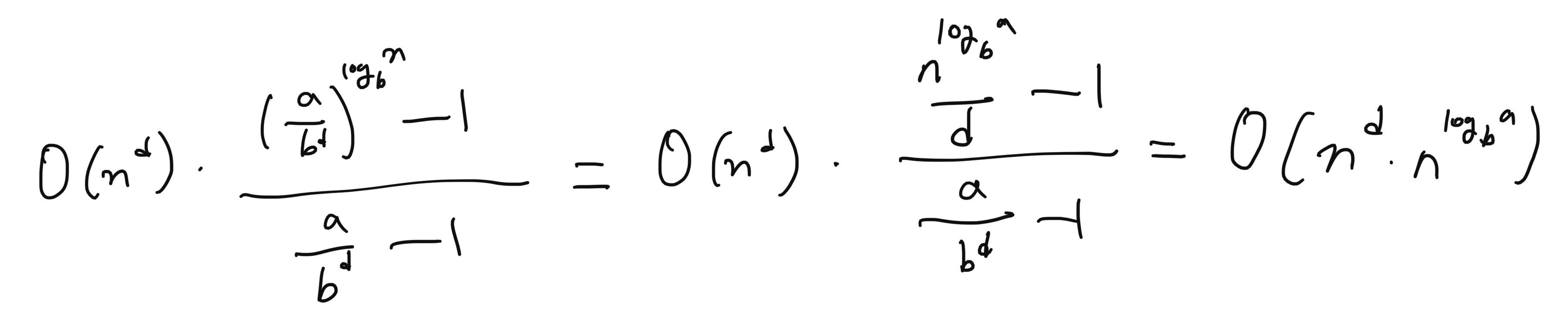
이 때, d > log_b(a) 이므로, 결국 O(n^d) 가 된다.

d < log_b(a)

위 그림과 똑같지만
d < log_b(a) 이므로, O(n^(log_b(a))가 된다.

d == log_b(a)

곱해지는 수가 1이면(d == log*b(a)), 총 합은 level * O(n^d) 이 된다.
r == 1이면 초항 * 개수이므로, 초항 = O(n^d), 개수는 level 수가 된다.
여기서 level = log_b(n), r = a/b^d 이므로,
log_b(n) * O(n^d)이므로 결국 O(log(n) * n^d)